The GISS V4 land/ocean temperature anomaly was 1.39°C in March, down from 1.44°C in February. This fall is smaller than the 0.11°C fall reported for TempLS.
As with TempLS, March was the warmest March in the record - next was 1.35°C in 2016. It was the fourth warmest month of all kinds.
As usual here, I will compare the GISS and earlier TempLS plots below the jump.
Friday, April 12, 2024
Monday, April 8, 2024
March global surface TempLS down 0.11°C from February, but still warmest March in record.
The TempLS FEM anomaly (1961-90 base) was 1.174°C in March, down from 1.284°C in February. It was still the warmest March in the record, just ahead of 1.138°C in 2016. The NCEP/NCAR reanalysis base index fell by 0.097°C.
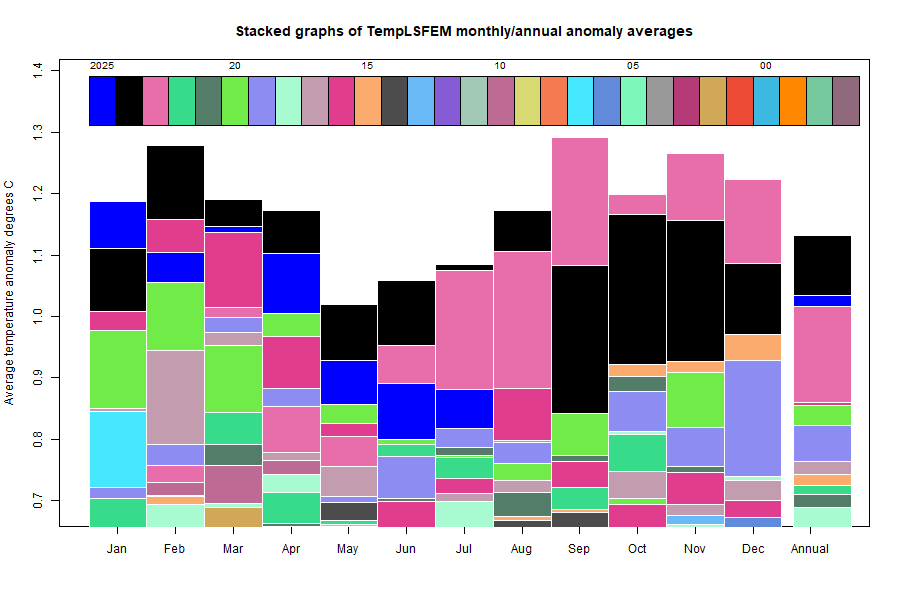
Here is the corresponding stacked graph, showing how much hotter recent months have been, as well as the now completed year of 2023:
Here is the temperature map, using the FEM-based map of anomalies. Use the arrows to see different 2D projections.
As always, the 3D globe map gives better detail. There are more graphs and a station map in the ongoing report which is updated daily.
Here is the corresponding stacked graph, showing how much hotter recent months have been, as well as the now completed year of 2023:

Here is the temperature map, using the FEM-based map of anomalies. Use the arrows to see different 2D projections.
As always, the 3D globe map gives better detail. There are more graphs and a station map in the ongoing report which is updated daily.
Wednesday, March 13, 2024
GISS February global temperature up by 0.22°C from January.
The GISS V4 land/ocean temperature anomaly was 1.44°C in February, up from 1.35°C in January. This rise is larger than the 0.165°C rise reported for TempLS.
As with TempLS, February was the warmest February in the record - next was 1.37°C in 2016.
As usual here, I will compare the GISS and earlier TempLS plots below the jump.
As with TempLS, February was the warmest February in the record - next was 1.37°C in 2016.
As usual here, I will compare the GISS and earlier TempLS plots below the jump.
Thursday, March 7, 2024
February global surface TempLS up 0.163°C from January; warmest February in record.
The TempLS FEM anomaly (1961-90 base) was 1.256°C in February, up from 1.093°C in January. It was the warmest February in the record, ahead of 1.16°C in 2016. The NCEP/NCAR reanalysis base index rose by 0.061°C.
It was very warm in N America, most of Europe, and the Arctic. Cold patches in Central Asia and far NE Siberia. Antarctica was cold.
Here is the temperature map, using the FEM-based map of anomalies. Use the arrows at bottom to see different 2D projections.
As always, the 3D globe map gives better detail. There are more graphs and a station map in the ongoing report which is updated daily.
Here is the updated stacked plot of monthly values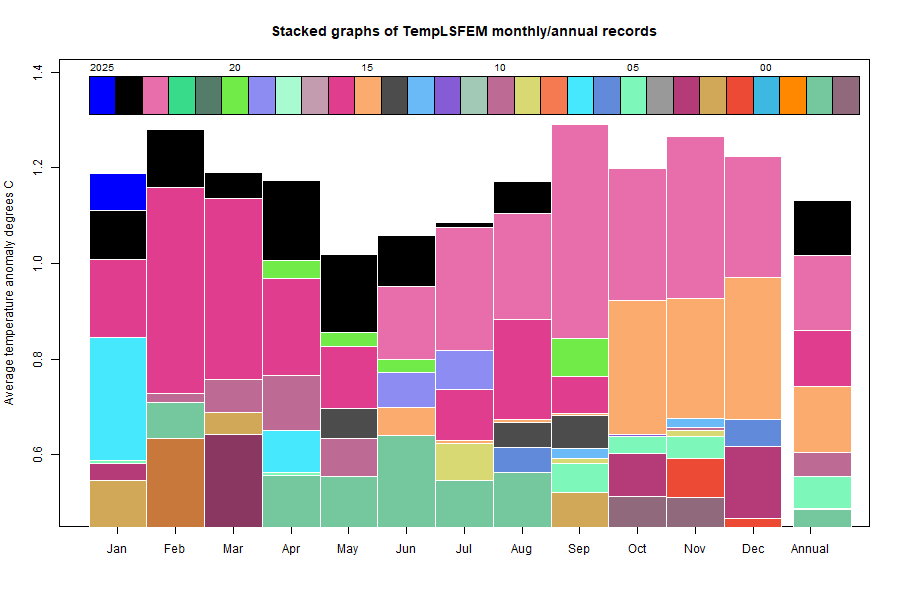
It was very warm in N America, most of Europe, and the Arctic. Cold patches in Central Asia and far NE Siberia. Antarctica was cold.
Here is the temperature map, using the FEM-based map of anomalies. Use the arrows at bottom to see different 2D projections.
As always, the 3D globe map gives better detail. There are more graphs and a station map in the ongoing report which is updated daily.
Here is the updated stacked plot of monthly values

Tuesday, February 13, 2024
GISS January global temperature down by 0.14°C from December.
The GISS V4 land/ocean temperature anomaly was 1.21°C in January, up from 1.35°C in December. This fall is similar to the 0.165°C fall reported for TempLS.
As with TempLS, January was still by a small margin the warmest January in the record - next was 1.18°C in 2016.
As usual here, I will compare the GISS and earlier TempLS plots below the jump.
As with TempLS, January was still by a small margin the warmest January in the record - next was 1.18°C in 2016.
As usual here, I will compare the GISS and earlier TempLS plots below the jump.
Wednesday, February 7, 2024
January global surface TempLS down 0.165°C from December, but still warmest January in record.
The TempLS FEM anomaly (1961-90 base) was 1.062°C in January, down from 1.227°C in December. It was still he warmest January in the record, but only just ahead of 0.982°C in 2016. This is the first time since May that the month was not warmest by a long way. The NCEP/NCAR reanalysis base index fell by 0.141°C.
It was very warm in NE N America, but cold in a band from the Gulf Coast to Alaska. Cold in N Europe and far East Siberia, but a band of warmth through N Africa to central Siberia. Antarctica was cold.
Here is the temperature map, using the FEM-based map of anomalies. Use the arrows at bottom to see different 2D projections.
As always, the 3D globe map gives better detail. There are more graphs and a station map in the ongoing report which is updated daily.
It was very warm in NE N America, but cold in a band from the Gulf Coast to Alaska. Cold in N Europe and far East Siberia, but a band of warmth through N Africa to central Siberia. Antarctica was cold.
Here is the temperature map, using the FEM-based map of anomalies. Use the arrows at bottom to see different 2D projections.
As always, the 3D globe map gives better detail. There are more graphs and a station map in the ongoing report which is updated daily.
Sunday, January 14, 2024
GISS December global temperature down by 0.06°C from November.
The GISS V4 land/ocean temperature anomaly was 1.37°C in December, down from 1.43°C in November. This fall is very similar to the 0.064°C fall reported for TempLS.
As with TempLS, December was still by a large margin the warmest December in the record - next was 1.16°C in 2015.
As usual here, I will compare the GISS and earlier TempLS plots below the jump.
As with TempLS, December was still by a large margin the warmest December in the record - next was 1.16°C in 2015.
As usual here, I will compare the GISS and earlier TempLS plots below the jump.
Subscribe to:
Posts (Atom)












